Transformée de Fourier et apodisation

Interferogrammes

Lors de l'analyse d'un échantillon par un spectrophotomètre infrarouge à transformée de Fourier (FTIR), le mode de mesure est normalement réglé sur la transmittance ou l'absorbance. Cependant, contrairement à un spectrophotomètre dispersif, l'instrument FTIR ne mesure pas directement ces spectres.
Dans les analyses FTIR, la lumière infrarouge de la source lumineuse passe à travers un interféromètre de Michelson le long du chemin optique.
L'interféromètre de Michelson comprend un séparateur de faisceau, un miroir mobile et un miroir fixe. Le faisceau lumineux, divisé en deux par le séparateur de faisceau, est réfléchi par le miroir mobile et le miroir fixe, avant d'être recombiné par le séparateur de faisceau.
Lorsque le miroir mobile effectue des mouvements de va-et-vient, la différence de chemin optique par rapport au miroir fixe change, de sorte que la différence de phase change avec le temps. Les faisceaux lumineux sont recombinés dans l'interféromètre de Michelson pour produire une lumière d'interférence. L'intensité de la lumière d'interférence est enregistrée dans un interférogramme, avec la différence de chemin optique enregistrée sur l'axe horizontal.
Les données directement acquises par l'instrument FTIR sont sous la forme d'un interférogramme de la lumière infrarouge qui a traversé l'échantillon. Observer l'interférogramme ne permet pas de comprendre les caractéristiques de l'échantillon. Pour obtenir un spectre normal avec le nombre d'ondes (longueur d'onde) sur l'axe horizontal, une transformée de Fourier par un ordinateur est nécessaire. C'est la principale caractéristique de l'instrument FTIR et ce qui le différencie d'un spectrophotomètre dispersif, qui mesure directement les spectres.

Principe de la Spectrophotométrie à Transformée de Fourier

Les données finales requises pour les mesures d'échantillons ont le nombre d'ondes sur l'axe horizontal, comme décrit ci-dessus.
Un spectre montre la lumière séparée en ses longueurs d'onde composantes et l'intensité tracée à chaque longueur d'onde.
Ce processus de séparation est appelé "spectroscopie".
Lorsque la lumière infrarouge à la longueur d'onde λ entre dans l'interféromètre de Michelson, si la différence de chemin optique est un multiple entier, les crêtes et les creux se superposent, augmentant l'intensité de la lumière. Inversement, lorsque la différence de chemin optique est un multiple demi-entier (entier + 1/2), la lumière devient plus faible. Si l'intensité lumineuse originale est notée P(λ), l'intensité I(x) à la différence de chemin optique x peut être exprimée comme suit

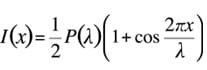
Dans la transformée de Fourier réelle, la composante AC (cos) dans l'expression ci-dessus forme l'interférogramme par rapport à la lumière infrarouge à la longueur d'onde λ.
Comme la lumière effectivement émise par la source lumineuse combine des lumières à diverses longueurs d'onde, l'interférogramme obtenu est la somme de l'expression ci-dessus à diverses longueurs d'onde λ.
Si la différence de chemin optique est nulle (0), la lumière est renforcée à toutes les longueurs d'onde, de sorte que l'interférogramme présente une intensité élevée. Cela s'appelle "burst central".
La transformée de Fourier est le processus de calcul de l'intensité de l'onde à chaque période à partir de la somme de toutes les périodes d'onde.
Appliquer une transformée de Fourier à un interférogramme permet d'obtenir l'intensité à chaque période, c'est-à-dire à chaque longueur d'onde.
Si un interférogramme I(x) pour la lumière infrarouge à des nombres d'ondes continus peut être créé en utilisant le nombre d'ondes ν au lieu de la longueur d'onde λ, I(x) peut être exprimé comme suit

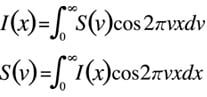
Où, S(ν) est l'intensité de la lumière infrarouge au nombre d'ondes ν.
S(ν) peut être calculé par transformée de Fourier.
Les données obtenues sont un spectre de puissance. Le rapport entre le spectre de puissance de fond et celui de l'échantillon produit un spectre exprimé en transmittance.

Apodisation

Comme décrit ci-dessus, un spectre de transmittance (ou un spectre converti en spectre d'absorbance) est obtenu lorsque la transformée de Fourier est appliquée à l'interférogramme mesuré.
Cependant, la description ci-dessus s'applique à une situation théorique. Les mesures réelles diffèrent de l'état idéal.
En particulier, la plage d'intégration pour l'expression ci-dessus est de 0 à l'infini. Cela supporte une plage de mouvement infinie du miroir mobile. Cependant, un tel mouvement est impossible. Le miroir mobile effectue des mouvements de va-et-vient sur une distance finie, de sorte que, en pratique, cette intégration doit être interrompue dans une plage finie.
Par exemple, si la plage d'intégration est restreinte à [-L, L], de sorte que les contributions en dehors de cette plage ne sont pas calculées, l'expression de la transformée de Fourier peut être écrite comme suit

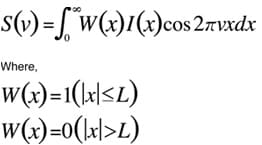
Quel effet ce calcul a-t-il sur le spectre S(ν) obtenu ? S(ν) incorpore des images de la transformée de Fourier de la fonction W(x). La transformée de Fourier de la fonction W(x) produit

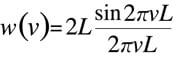
Des ondulations se forment autour d'un grand pic.

Forme d'onde en boîte W(x) et w(ν)

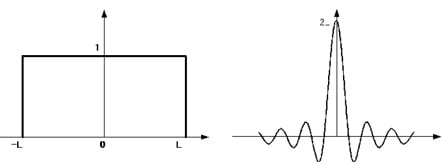
Incorporer w(ν) dans le spectre S(ν) entraîne des ondulations comme W(x) autour d'un pic dans le spectre. Pour une forme d'onde en boîte simple comme W(x) ci-dessus, la plus grande ondulation après le pic est la vallée adjacente, qui a une profondeur d'environ 21 % de la hauteur du pic. Si les ondulations sont grandes, le spectre obtenu contient des irrégularités analogues à des pics, et il différera du spectre réel.
Cependant, si nous utilisons une forme d'onde triangulaire au lieu d'interrompre soudainement le calcul dans la plage d'intégration, nous obtenons

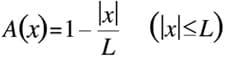
Si cela est utilisé à la place de W(x) ci-dessus, l'image de la transformée de Fourier a(ν) devient

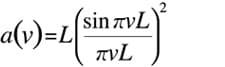
Forme d'onde triangulaire A(x) et a(ν)

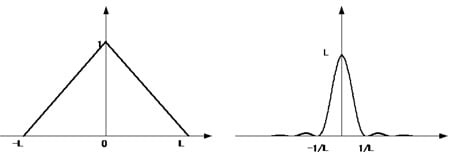
À première vue, il est évident que les ondulations sont plus petites.
C'est parce que l'intégration n'est pas soudainement interrompue à la limite. Au lieu de cela, les contributions diminuent à un taux constant à mesure que la limite est atteinte.
Cependant, le pic central est également plus bas et quelque peu plus large. Cela apparaît comme une résolution réduite dans le spectre réel.
Appliquer un type de fonction à l'intégration de la transformée de Fourier pour réduire les ondulations, comme dans cet exemple, est appelé "apodisation" et la fonction est connue sous le nom de "fonction d'apodisation". Il peut être vu à partir des exemples de la forme d'onde en boîte et de la forme d'onde triangulaire que réduire les ondulations implique un compromis entre la résolution et la hauteur du pic. Améliorer l'un rend l'autre pire. Par conséquent, la fonction d'apodisation doit être choisie en fonction de l'objectif visé.
La fonction Happ-Genzel est souvent utilisée pour obtenir un bon équilibre entre la taille des ondulations et la résolution.

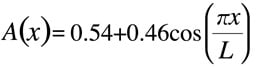
Son application à l'image de la transformée de Fourier donne

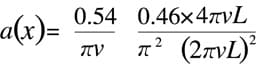
Happ-Genzel A(x) et a(ν)

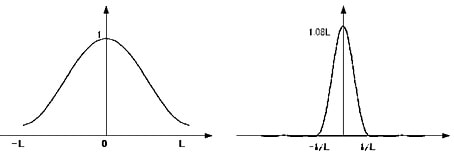
L'image de la transformée de Fourier montre un pic central élevé et des ondulations bien supprimées.
La fonction Happ-Genzel est normalement utilisée. Cependant, dans les cas où une bonne résolution est requise, comme les mesures de gaz, la fonction en boîte est utilisée.
Les fonctions d'apodisation doivent être séparées en fonction de l'objectif visé, comme indiqué ci-dessus.

Annexe : Principales Fonctions d'Apodisation

Remarque) La résolution s'applique à une diminution de 2 % par rapport à la hauteur du pic. La valeur de l'ondulation exprime une proportion de la hauteur du pic.

Errata
Annexe : Principales Fonctions d'Apodisation
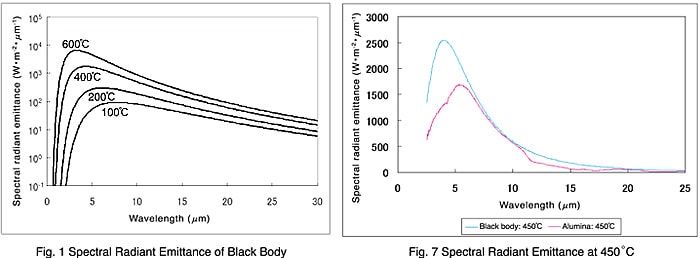
Des diagrammes incorrects sont apparus dans l'article "Mesure de l'émissivité spectrale en utilisant la spectrophotométrie FTIR"
dans FTIR TALK LETTER Vol. 13.
Nous nous excusons pour le désagrément. Veuillez remplacer les diagrammes comme suit.
Remplacez les Fig. 1 et Fig. 7 par les diagrammes ci-dessous.