Méthode de réflexion spéculaire et analyse de Kramer-Koenig
La lumière qui se réfléchit à l'angle d'incidence est connue sous le nom de "lumière de réflexion spéculaire". La méthode FTIR qui exploite la lumière de réflexion spéculaire est appelée "méthode de réflexion spéculaire". Lors de l'utilisation de la méthode de réflexion spéculaire, l'échantillon peut être irradié avec de la lumière infrarouge sous un angle d'incidence presque vertical ou presque horizontal. Un accessoire de réflexion spéculaire qui irradie l'échantillon avec de la lumière infrarouge sous un angle vertical est utilisé pour mesurer les spectres infrarouges de revêtements métalliques relativement épais, de l'ordre du µm, ou pour mesurer l'épaisseur du film sur des plaquettes épitaxiales en utilisant des franges d'interférence.
Cependant, lorsque un spectre de réflexion spéculaire est mesuré pour des échantillons brillants qui présentent une absorption dans la plage infrarouge, tels que le plastique, le verre ou le cristal, les pics sont déformés vers la forme différentielle du premier ordre en raison de la dispersion anormale de l'indice de réfraction dans une plage où l'absorption se produit. L'analyse de qualification ou de groupe fonctionnel est difficile à partir d'un tel spectre. Par conséquent, le spectre déformé doit être converti en un spectre d'absorption normal en utilisant la transformation dite de Kramers-Koenig.
(1) Analyse de Kramers-Koenig
L'explication ci-dessous s'applique à l'irradiation de la substance à un angle d'incidence presque vertical. Une explication plus détaillée est donnée dans les Références 1), 2) ci-dessous. L'indice de réfraction complexe de la substance n* est défini comme suit :
n*= n + ik (où n et k sont respectivement l'indice de réfraction et le coefficient d'absorption de la substance)
Ensuite, la réflectance d'amplitude (r) sous irradiation verticale et la réflectance d'énergie (R) déterminée directement à partir du spectre de réflexion spéculaire sont exprimées par les équations suivantes :
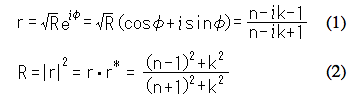
Où, φ est le changement de phase. Cela résulte du fait que la réflexion et l'absorption se produisent à la surface de l'échantillon. r* est le conjugué complexe de r.
Diviser l'Équation (1) en parties réelle et imaginaire et résoudre pour n et k donne les équations suivantes :
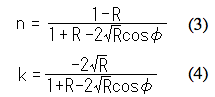
Prendre le logarithme de l'Équation (1) donne
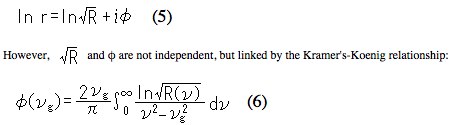
Si la réflectance d'énergie est mesurée sur toute la plage de nombres d'onde, le changement de phase φ(νg) peut être calculé à n'importe quel nombre d'onde requis νg en utilisant cette expression relationnelle, puis les constantes optiques n et k peuvent être déterminées à partir des Équations (3) et (4). Par conséquent, en calculant k à des intervalles de nombres d'onde constants dans la plage infrarouge normale entre 4600 et 400 cm-1, par exemple, un spectre de coefficient d'absorption équivalent au spectre de transmission peut être calculé à partir du spectre de réflexion spéculaire.
Dans l'intégration de l'Équation (6), un pôle existe à ν = νg mais plusieurs méthodes ont été proposées pour gérer cette intégration. Deux méthodes typiques sont la méthode de Maclaurin et la méthode de transformation de Fourier double. Dans la méthode de Maclaurin, le changement de phase φ(νg) est donné par l'Équation (7)
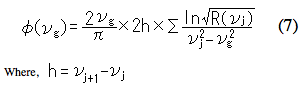
j = 2, 4, 6, ........., g-1, g+1, ......... (si g est un nombre impair)
j = 1, 3, 5, ........., g-1, g+1, ......... (si g est un nombre pair)
Le point de départ νj est défini de sorte que ν = νg ne se produise pas et des points de données alternés sont utilisés. Avec la méthode de transformation de Fourier double, φ(νg) est déterminé par l'Équation (8), une transformation de Fourier double qui est une approximation de l'Équation (6).
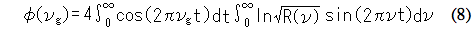
La méthode de Maclaurin fournit une meilleure précision de calcul, mais comme elle est très chronophage, la méthode de transformation de Fourier double, plus rapide, est normalement utilisée.
(2) Accessoire de Réflexion Spéculaire
La Fig. 1 montre l'apparence de l'accessoire de réflexion spéculaire SRM-8000. La Fig. 2 montre le système optique. La lumière réfléchie par les miroirs plans M1 et M2 se réfléchit sur le miroir sphérique M3 et forme une image sur la surface de l'échantillon. Le faisceau lumineux a un angle d'incidence moyen de 10 degrés par rapport à l'échantillon. La lumière réfléchie par l'échantillon se réfléchit sur le miroir sphérique M4 et les miroirs plans M5 et M6 vers le détecteur dans l'instrument FTIR.
Les références normales sont un miroir en aluminium et un miroir déposé par vaporisation en or.

Fig. 1 Apparence de l'Accessoire de Réflexion Spéculaire SRM-8000
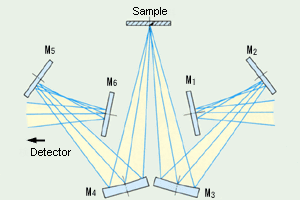
Fig. 2 Système Optique de l'Accessoire de Réflexion Spéculaire SRM-8000
(3) Exemples de Mesures
La Fig. 3 montre le spectre de réflexion spéculaire pour une feuille d'acrylique. Il présente une absorption jusqu'à 2000 cm-1 mais les pics sont déformés vers la forme différentielle du premier ordre en raison de la dispersion anormale de l'indice de réfraction. La Fig. 4 montre le spectre de la Fig. 3 après la transformation de Kramers-Koenig. Ce spectre indique que l'échantillon est du polyméthacrylate de méthyle (PMMA).
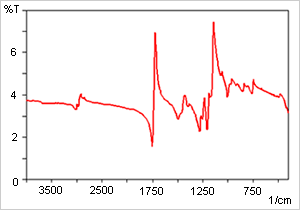
Fig. 3 Spectre de Réflexion Spéculaire pour le Polyméthacrylate de Méthyle (PMMA)
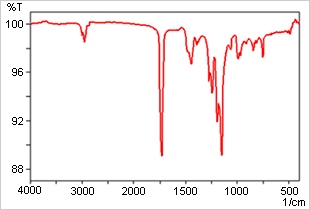
Fig. 4 Spectre de Réflexion Spéculaire pour le Polyméthacrylate de Méthyle (PMMA) après Transformation de Kramers-Koenig
|
Références
|






